Getting started
SQLite is a common SQL database engine. In this blog, I will go over how you can connect and query a SQLite database in Python.
Let’s import the necessary libraries for this example, and establish a connection to a database. We will be using the sqlite3 library and pandas.
import sqlite3
import pandas as pd
conn = sqlite3.connect('supermarket.db') # connect to a supermarket databaseTo execute SQL commands, we need to create a cursor object. Let’s use the cursor to create a table called shops which will contain basic information about our supermarket stores (shop ID, size, postcode) . The store sizes are small, medium and large.
cursor = conn.cursor() # create a cursor
cursor.execute("CREATE TABLE shops(shopid VARCHAR(100) PRIMARY KEY, Store_size VARCHAR(30), Postcode VARCHAR(8))")So, cursor.execute() executes SQL commands.
We can insert data into the table using the INSERT command. If we do this, use conn.commit() to save the data to the table.
However, in this example, we have a pandas DataFrame called shops_df that we wish to insert into our SQL table called shops. It has the same columns as our shops table. If you’re more familiar with pandas than SQL like me, I will use pandas to clean data first. Only after this will I want to store the data in an SQL database.
The to_sql() function allows us to write records in a DataFrame to an SQL database.
shops_df.to_sql('shops', conn, if_exists='append', index=False) # write shops_df to shops tableQueries
The cursor behaves like an iterator object. We can use a for loop to retrieve all rows from a SELECT statement. To make it easier to query in future, I’ll create a query function.
def query(q):
try:
for row in cursor.execute(q):
print(row)
except Exception as e:
print("Something went wrong... ", e)
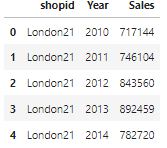
query('SELECT * FROM shops')We can also save the results of a query by assigning it to a variable. The variable will be a list of tuples. A tuple for each row.
q="SELECT shopid, Postcode FROM shops"
query_results = cursor.execute(q).fetchall() # save results as a list of tuplesStoring results from a query like this can allow you to represent table data with graphs. For example, if you had a table called sales in your database which has the shop profits, you could plot trends in sales. I will illustrate this now.
Let’s query the minimum, mean and maximum yearly sales…
c="""
SELECT shops.Store_size, sales.Year, MIN(sales.Sales), AVG(sales.Sales), MAX(sales.Sales)
FROM shops
JOIN sales
ON shops.shopid = sales.shopid
GROUP BY shops.Store_size, sales.Year
"""
query(c)
result = cursor.execute(c).fetchall()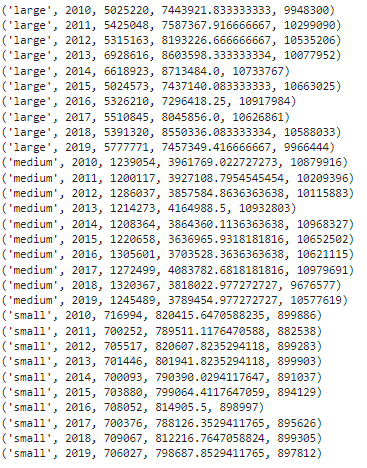
…next I plot the mean sales for medium sized stores against the year…
years=[] # store the year
means = [] # store the mean sales
size = 'medium'
for results in result:
if results[0] == size:
means.append(results[3])
years.append(results[1])
plt.plot(years, means, linestyle = 'dashed', marker = 'o', ms= '5')
plt.title(f"{size} store mean sales")
plt.xlabel("year")
plt.ylabel("sales")
plt.savefig(f"{size}_store_mean_sales.png")
plt.show()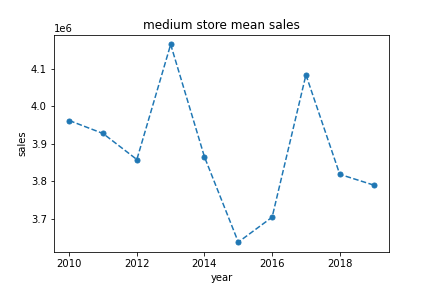
Now we are done, close the connection to the database.
conn.close() # don't forget to close the connection afterwardsI hope this blog was helpful for getting started with the sqlite3 library, to connect to a database, and use a cursor to execute SQL commands in python.